Pada awalnya program linear dikembangkan oleh W.W. Leontife,seorang ahli ekonomi, yang berupa analisis dari metode input-output(metode masukan dan keluaran). Kemudian dilanjutkan Hitchock (1941) dan Koopmans (1947) yang mempelajari masalah transportasi. Selanjutnya G.B. Dantzig (1948) memperkenalkan sebuah metode yang dapat digunakan untuk menentukan solusi optimum yang sering disebut dengan metode simpleks.
Dalam sebuah perusahaan sering menggunakan program linear ini untuk menyelesaikan masalah pengoptimalan yang mereka hadapi, seperti pemaksimalan keuntungan, peminimuman biaya produksi dan sebagainya. Misalkan sebuah perusahaan roti ingin memproduksi dua jenis roti. Setiap jenis roti memerlukan bahan tepung dan mentega. Jenis roti I membutuhkan 200 gram tepung dan 75 gram mentega, sedang jenis roti II membutuhkan 100 gram tepung dan 50 gram mentega. Jika tersedia 100 kg tepung dan 25 kg mentega berapa roti jenis I dan jenis II yang dapat dibuat supaya memperoleh jumlah yang sebanyak-banyaknya, sedang untuk bahan yang lain cukup tersedia? Contoh di atas adalah salah satu persoalan yang menyangkut program linear. Untuk menyelesaikan masalah tersebut, soal harus diterjemahkan lebih dahulu dalam model matematika.
Model Matematika
Dalam menyelesaikan masalah yang menyangkut program linear, model matematika sangat dibutuhkan. Dalam model matematika nantinya akan terlihat fungsi tujuan dan fungsi batasan. Fungsi tujuan adalah fungsi yang menunjukkan sasaran dari pengoptimalan yang mungkin dicapai berdasar batasan-batasan yang ada. Agar kalian lebih memahami tentang model matematika dan cara pembuatannya perhatikan beberapa contoh berikut ini.
Contoh
- Seorang pedagang sepeda ingin membeli sepeda balap dan sepeda motor sebanyak 25 buah untuk persediaan. Harga sebuah sepeda balap Rp1.500.000,00 dan sepeda motor Rp8.000.000,00. Jika modal yang dimiliki Rp100.000.000,00 buatlah model matematika dari permasalahan tersebut.
- Ali menjual es krim dalam termos yang paling banyak memuat 500 bungkus. Harga es krim jenis I Rp2.000,00 dan jenis II Rp1.000,00. Jika modal yang tersedia Rp1.100.000,00 dan laba masing-masing jenis es krim Rp200,00 dan Rp250,00 buatlah model matematika untuk permasalahan tersebut.
- Makanan A dibuat dari 4 ons tepung dan 2 ons mentega, sedangkan makanan B dibuat dari 3 ons tepung dan 3 ons mentega. Pengusaha makanan mempunyai 6 kg tepung dan 4,5 kg mentega. Jika harga makanan A Rp5.000,00 per buah dan makanan B Rp3.000,00 per buah, tentukan model matematika dari permasalahan tersebut.
Penyelesaian pertama
Untuk memudahkan dalam membuat model matematika dari permasalahan di atas, terlebih dahulu disusun dalam sebuah tabel yang menggambarkan unsur-unsur yang ada.
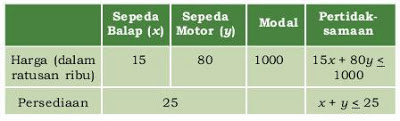
Misalkan banyaknya sepeda balap yang mungkin dibeli x buah dan sepeda motor ybuah, dengan demikian tabel pemodelannya ditunjukkan sebagai berikut.
Model matematika dari permasalahan di atas adalah:
15x + 80y < 1000
x + y < 25
Karena banyak sepeda tidak mungkin negatif maka harus ditambahkan syarat nonnegatif.
x > 0
y > 0,
dengan x,y cacah.
Penyelesaian Kedua
Misalkan banyaknya es krim jenis I yang mungkin dijual x buah dan es krim jenis II y buah. Tabel pemodelannya sebagai berikut.
Model matematika dari permasalahan di atas adalah:
2000x + 1500y < 1.100.000
x + y < 500
Karena banyak es krim tidak mungkin negatif, maka harus diberikan syarat bahwa:
x>0
y>0,
(syarat nonnegatif)
Dengan fungsi tujuan memaksimumkan 200x+ 150y ; x, y cacah
Penyelesaian Ketiga
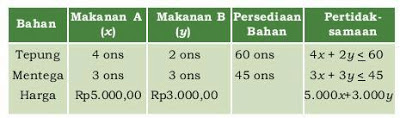
Misalkan banyaknya makanan A yang mungkin dibuat x buah dan makanan B ybuah. Tabel pemodelan masalahnya sebagai berikut.
Model matematika dari permasalahan tersebut adalah:
4x + 2y < 60
3x + 3y < 45
Karena banyak makanan tidak mungkin negatif maka harus ditambahkan syarat nonnegatif yaitu:
x, y>0
(syarat nonnegatif)
Dengan fungsi tujuan memaksimumkan 5.000x + 3.000y ; x, y cacah.
sumber : Buku BSE Matematika Aliyah karya Pangarso Y dan Dewi Retno














0 komentar:
Posting Komentar